On the previous webpage we concerned ourselves with motion in one dimension. We now add a dimension and deal with the motion of objects in two dimensions. This means the motion we are concerning ourselves with can be described along two axes. In tradition these are the x axis and the y axis. To study the motion of objects in more than one dimension we need to first discuss vectors and the mathematical operations that are involved with them. So, lets just dive into the mterial. We begin below with a treatment of Vectors and Scalars.
As mentioned in the previous section, in physics, the terms velocity and acceleration refer not only to fast or "quick" something is moving but in what direction it is moving. A quantity that incorporates both magnitude and direction is called a vector. However, not all quantities incorporate both of these properties. Some quatities, like mass and temperature, have only a magnitude assocaited with them. These quantities are called scalars.
Now, when dealing with vectors it is often helpful to draw a diagram depicting the physical situation the vectors describe. On a diagram each vector is represented by an arrow. The arrow is drawn so that it points in the direction of the vector quantity it represents. The length of the arrow is drawn to be proportional to the magnitude of the vector quantity. When we write the symbol for a vector it will be done so in boldface type. Thus, for example, we write v for velocity. Vectors in handwritten work, and sometimes in type, are often indicated with a little arrow over the top of the quantity symbol. If we are specifying only the magnitude of the quantity it will be done so simply in italics, as it was all through the last webpage.
Now, I have skipped what most physics text books do cover expressly. That is the addition and subtraction of vectors graphically. This can be done by tediously drawing a diagram to scale and measuring out the vectors carefully. I personally feel that vector operations such as addition and subtraction can be done so much more easily, efficiently, and proned less to error if done so using components. All you really need to take from what I have skipped that you must know is that a vector can be multiplied by a scalar. But this too can be done component by component. With that said, lets take a look at vector operations using components.
Consider first a vector V that lies in a particular plane. It can be expressed as the sum of two other vectors, called the components of the original vector. The components are usualyy chosen to be along two perpendicular directions. The process of finding the components is known as resolving the vector into its components. Consider the figure below.
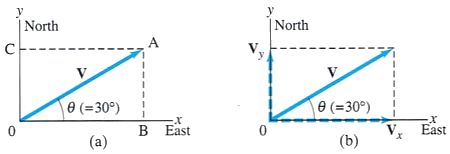
The vector V could be a displacement vector that points at an angle θ = 30o north of east, where we have chosen the positive x axis to be to the east and the positive y axis north. This vector V is resolved into its x and y components by drawing dashed lines from the tip (A) of the vector and drawing these lines perpendicular to the x and y axes (lines AB and AC). Then the lines OB and OC represent the x and y components of V, respectively, as shown in part (b) of the figure. These vector components are written Vx and Vy. We generally show vector components as arrows, like vectors, but dashed. The scalar components, Vx and Vx, are numbers, with units, that are given a positive or negative sign depending on whether they point along the positive or negative x and y axis. Obviously, Vx + Vy = V.
Space is made up of the dimensions, and sometimes it is necessary to resolve a vector into components along
three mutually perpendicular directions. In rectangular coordinates the components are Vx,
Vy, and Vz, so
V = Vx + Vy + Vz. Resolution
of a vector in three dimensions is merely an extension of the above illustration in the two dimensional case.
We will mostly be concerned with working with vectors in a plane which only require two components though.
Trigonometric functions can be used to find the components of a vector. A vector and its two components can be thought of as making up a right triangle. We then see that the sine and cosine of the angle between the positive x axis and the vector can be multiplied by the magnitude of the vector to obtain the magnitudes of the x and y components, respectively. The calculations are as follows:
As is obvious with a little analysis of the above equations, the magnitude of the vector in question can be found if the angle and either the x or y components are known. Also, the magnitude of the vector can be found if the x and y components of the vector are known using the theorem of Pythagoras. Oh, and lest we forget, if the conponents are known the angle can also be found using the definition of tangent. The equations below show how this is done.
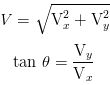
We can now discuss the addition of vectors using components. The first step is to resolve each vector into its components. Next we add each component wise. Imagine we have two vectors resolved into its components as shown below.
The resultant vector from the addition of V1 to V2, V, would then be as follows:
where
So, the sum of the x components equals the x component of the resultant, and similarly for the y component. Please bear in mind that we do not add x components to y components. As shown earlier the theorem of Pythagoras and the trigonometric tangent function can be used to find the magnitude and direction of the resultant vector, respectively. Ok, with this part explained lets try an example.
A rural mail carrier leaves the post office and drives 22.0 km in a northerly direction to the next town. She then drives in a direction 60.0o south of east for 47.0 km to another town. What is her displacement from the post office?
SOLUTION We want to find her resultant displacement from the origin. We choose the positive x axis to be east and the positive y axis north, and resolve each displacement vector into its components. Let D1 be the displacement vector from the origin to the first town pointing up the y axis, which is north. Let D2 be the displacement vector from the first town to the second town, which is, as was stated, 60.0o south of east. Since D1 has magnitude 22.0 km and points north, it only has a y component:
whereas D2 has both x and y components:
Notice that D2y is negative because this vector points along the negative y axis. The resultant vector, D, has components:
This specifies the resultant vector completely:
We can also specify the resultant vector by giving its magnitude and angle as follows:

The negative sign means θ = 38.5o below the x axis.
Vectors can be conveniently written in terms of unit vectors. A unit vector is defined to have a magnitude of exactly one. It is useful to define unit vectors that point along coordinate axes, and in a rectangular coordinate system these unit vectors are called i, j, and k. They point, respectively, along the positive x, y, and z axes. Any vector V can be written in terms of its components as follows:
So, as you can guess, two vectors can be added as follows:
We can now extend our definitions of velocity and acceleration in a formal way to two, and even three, dimensional motion. Suppose a particle follows a path in the xy plane. At a time t1, the particle is at a point P1, and at a time t2, it is at a point P2. Imagine a vector r1. This vector is the position vector of the particle at the time t1. Now as you can guess, r2 is the position vector at the time t2.
In one dimenison, we defined displacement as the change in position of the particle. In the more general case of two or three dimensions, the displacement vector is defined as the vector representing change in position. We call it Δr, where
This represents the displacement during the time intervel Δt = t2 - t1. In unit vector notation, we can write
where x1, y1, and z1 are the coordinates of point P1. Similarly,
Hence
If the motion is along the x axis only, then y2 - y1 = 0, z2 - z1 = 0, and the magnitude of the displacement is Δr = x2 - x1, which is consistent with our one-dimensional equation from the previous webpage. Even in one dimension, displacement is a vector, as are velocity and acceleration.
The average velocity vector over the time intervel Δt = t2 - t1 is defined as follows:
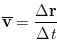
Since v is a product of the vector Δr times a scalar (1 / Δt), the direction of v is the same as that of Δr; and its magnitude Δr / Δt.
We next consider shorter and shorter time intervels - that is, we let &Delat;t approach zaro so that the distance between points P2 and P1 also approaches zero. We define the instantaneous velocity vector as the limit of the average velocity as Δt approaches zero:
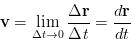
The instantaneous velocity is equal to the derivative of the position vector with respect to time. The above equation can be written in terms of components as follows:
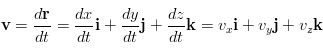
Acceleration in two or three dimensions is treated in a similar way. The average acceleration vector over a time intervel Δt = t2 - t1 is defined as follows:
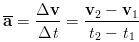
The instantaneous acceleration vector is defined as the limit of the average acceleration vector as the time intervel Δt is allowed to approach zero as follows:
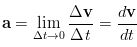
And is thus the derivative of v with respect to t. Using components gives us the following:
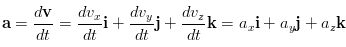
On the last webpage we studied the motion of objects in one dimension in terms of displacement, velocity, and acceleration, including purely vertical motion of falling bodies undergoing acceleration due to gravity. Now we examine the more general motion of objects moving through the air in two dimensions near the surface of the Earth, such as a gold ball, a thrown or batted baseball, kicked footballs, speeding bullets, and athletes doing the long jump or high jump. These are all examples of projectile motion, which we can describe as taking place in two dimensions. Although air resistance is often importent, in many cases its effect can be ignored, and we will ignore it in the following analysis. We will not be concerned now with the process by which the object id thrown or projected. We consider only its motion after it has been projected and is moving freely through the air under the action of gravity alone. Thus the acceleration of the object is that due to gravity, which acts downward with magnitude g = 9.80 m/s2, and we assume it is constant.
Galileo first accurately described projectile motion. He showed that it could be understood by analyzing the horizontal and vertical components of the motion seperately. For convenience, we assume that the motion begins at time t = 0 at the origin of an xy coordinate system (so x0 = y0 = 0).
Let's consider a tiny ball rolling of the end of a table with an initial velocity vx0 in the horizontal (x) direction. Imagine we are looking at the velocity vector v of the ball once it leaves the table's edge. This velocity vector will point in the direction of motion of the ball at every point along the way. Following Galileo's idea's, we treat the horizontal and vertical components of the velocity, vx and vy, seperately, and we can apply the kinematic equations learned from the previous webpage to each.
First we examine the vertical (y) component of the motion. Once the ball leaves the table, it experiences a vertically downward acceleration, g, the acceleration due to gravity. Thus vy is initially zero (vy0) but increases continually in the downward direction (until the ball hits the ground). Let us take y to be positive upwards. Then ay = -g, and we can write vy = -gt since we set y0 = 0.
In the horizontal direction, on the other hand, there is no acceleration. So the horizontal component of velocity, vx, remains constant, equal to its initial value, vx0, and thus has the same magnitude at each point on the path. The two vector components, vx and vy, can be added vectorially to obtain the velocity v for each point on the path.
One result of this analysis, which Galileo himself predicted, is that an object projected horizontally will reach the ground in the same time as an object dropped vertically. This is because the vertical motions are the same in both cases.
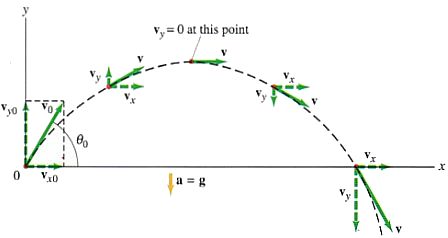
Consider the figure above. If an object is projected at an upward angle the analysis is similar to that of the situation just described earlier, except now there is an initial vertical component of velocity, vy0. Because of the downward acceleration of gravity, vy continually decreases until the object reaches the highest point on its path, at which point vy = 0. Then vy starts to increase in the downward direction, as shown in the figure (that is, becoming negative). As before, vx remains constant.
Galileo's analysis of almost four centuries ago is exactly equivalent to using the kinematic equations presented on the last webpage seperately for the horizontal (x) and vertical (y) components. The constant acceleration now is that of gravity alone, acting downward. As can be seen in the above figure for an object projected at an upward angle θ, the acceleration is in one (constant) direction, whereas the velocity has two components, one of which (vy) is continuously changing, whereas the other (vx) stays constant.
We can simplify the kinematic equations presented previously for use with projectile motion by setting
ax = 0. If we assume y is postive upward ay = -g =
-9.80 m/s2. Note also that if θ is chosen as in the last figure then the initial
velocity has the following components:
A movie stunt car driver on a motorcycle speeds horizontally of a 50.0 m high cliff. How fast must the motorcycle leave the cliff-top if it is to land on level ground below, 90.0 m from the base of the cliff where the camera's are?
SOLUTION We take the y direction to be positive upward, with the top of the cliff as y0 = 0, so the bottom is at y = -50.0 m. First, we find how long it takes the motorcycle to reach the ground below. For the vertical (y) direction we use one of the kinematics equations from the previous webpage with y0 = 0, and vy0 = 0 and get the following:We solve for t and set y = -50.0 m:
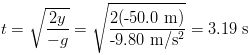
To calculate the initial velocity, vx0, we again use a kinematics equation from the previous webpage, but this time for the horizontal (x) direction we set ax = 0 and x0 = 0:
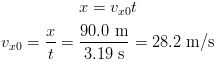
A football is kicked at an angle θ0 = 37.0o to the ground and with a velocity of 20.0 m/s. Calculate (a) the maximum height, (b) the time of travel before the football hits the ground, (c) how far away it hits the ground, (d) the velocity vector at the maximum height, and (e) the acceleration vector at the maximum height. Assume the ball leaves the foot at ground level, and ignore air resistance.
SOLUTION We take the y direction as positive upward. The components of the initial velocity are as follows:(a) At the maximum height, the velocity is horizontal, so vy = 0; and this occurs at time
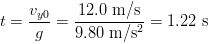
And with y0 = 0 we have
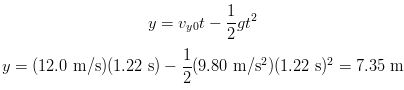
(b) To find the time it takes for the ball to return to the ground we can proceed as follows:
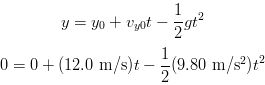
This equation can easily be factored and solved as follows:
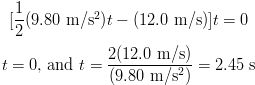
The first solution, t = 0, corresponds to the initial point, y0, and the second to when the ball hits the ground.
(c) The total distance traveled in the x direction is found as follows:
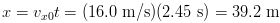
(d) At the highest point, there is no vertical component to the ball's velocity. There is only a horizontal component (which remains constant throughout flight), so the answer is as follows:
(e) The acceleration vector is the same at the highest point as it is throughout the flight, which is 9.80 m/s2 downward.
(a) Derive a formula for the horizontal range R of a projectile in terms of its initial velocity v0 and angle θ0. The horizontal range is defined as the horizontal distance the projectile travels before returning to its original height, which is typically the ground; that is, yfinal = y0. (b) Suppose one of Napolean's cannons had a muzzle velocity, v0, of 60.0 m/s. A what angle should it have been aimed to strike a target 320 m away?
SOLUTION (a) We set x0 = 0 and y0 = 0 at t = 0. After the projectile travels a horizontal distance R, it returns to the same level, y = 0, the final point So, to find a general expression for R, we set both y = 0 and y0 = 0 for the vertical motion, and obtain the following:We solve for t, which gives two solutions: t = 0 and t = 2vy0/g. The first solution corresponds to the initial instant of projection and the second is the time when the projectile returns to y = 0. Then the range, R, will be equal to x at the moment t has this value, which we put into one of our kinematics equations for the horizontal motion. Thus we have:
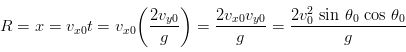
Here we have written vx0 = v0 cos θ0 and vy0 = v0 sin θ0. This is the result we sought, and it can be rewritten, using the trigonometric identity 2 sin θ cos θ =
sin 2θ, as
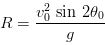
We see that the maximum range, for a given initial velocity v0, is obtained when the sine function takes on its maximum value of 1.0, which occurs for 2θ0 = 90o; so
Note that the maximum range increases by the square of v0, so doubling the muzzle velocity of a cannon increases its maximum range by a factor of 4.
(b) From the equation we just derived, Napolean's cannon should be aimed at an angle θ0 given by the following:
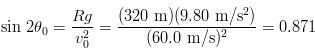
We want to solve for an angle θ0 that is between 0o and 90o, which means 2θ0 in this equation can be as large as 180o. Thus, 2θ0 = sin-1 0.871 = 60.6o is a solution, but 2θ0 = 180o - 60.6o = 119.4o is also a solution. In general we will have two solutions, which in Napolean's case are given by the following:
Either angle gives the same range. Only when sin 2θ0 = 1 (so θ0 = 45o) is there a single solution (that is, both solutions are the same).
An object that moves in a circle at a constant speed v is said to undergo uniform circular motion. Examples are a ball on the end of a string revolved about one's head, and the nearly uniform circular motion of the Moon around the Earth. The magnitude of the velcoity remains constant in this case, but the direction of the velocity is continually changing. Since accleration is defined as the rate of change of velocity, a change in direction of velocity means an accleration is occuring, just as does a change in magnitude. Thus an object undergoing uniform circular motion is accelerating even if the speed remains constant. We can now take a look at this accleration quantitatively.
If you recall, acceleration is defined as follows:
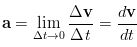
Δv is the change in velocity during the short time interval Δt. We will eventually consider the situation when Δt approaches zero an thus obtain the instantaneous acceleration. But for purposes of making a clear drawing we consider a nonzero time interval. Now take a look at the diagram below.
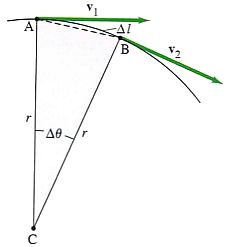
During the time Δt the particle in the diagram moves from point A to point B, covering a small distance Δl along the arc which subtends the small angle Δθ. The change in the velocity vector is v2 - v1 = Δv.
If we let Δt be very small (approaching zero), then Δl and Δθ are also very small; then v2 will be almost parallel to v1 and v will be essentially perpendicular to them. Thus Δv points toward the center of the circle. Since a, by definition, is in the same direction as Δv, it too must point toward the center of the circle. Therefore, this acceleration is called centripetal acceleration ("center seeking" acceleration) or radial acceleration (since it is directed along the radius toward the center of the circle), and we denote it by aR.
We next determine the magnitude of the radial acceleration, aR. Because CA is perpendicular to v1, and CB is perpedicular to v2, it follows that the angle Δθ, defined as the angle between CA and CB, is also the angle between v1 and v2. Hence the vectors v1, v2, and Δv form a triangle that is geometrically similar to triangle CAB. Taking Δθ small (letting Δt be very small) and setting v = v1 = v2 because the magnitude of the velocity is assumed not to change, we can write the following:
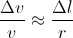
This is an exact equality when Δt approaches zero, for then the arc length Δl equals the cord length AB. Since we want to find the instantaneous acceleration, for which Δt approaches zero, we write the above expression as an equality and solve for Δv:
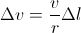
To get the centripetal acceleration, aR, we divide Δv by Δt:
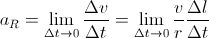
And since
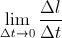
is the speed, v, of the object, we get
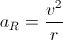
To summarize, an object moving in a circle of radius r with constant speed v has an acceleration whose direction is toward the center of the circle and whose magnitude is aR = v2 / r. It is not surprising that this acceleration depends on v and r. For the greater the speed v, the faster the velocity changes direction; and the larger the radius, the less raqidly the velocity changes direction.
The acceleration vector points toward the center of the circle. Bu the velocity vector always points in the direction of motion, which is tangential to the circle. Thus the velocity and acceleration vectors are perpendicular to each other at every point in the path for uniform circular motion. This is another example that illustrates the error in thinking that acceleration and velocity are always in the same direction. For an object falling vertically, a and v are indeed parallel. But in circular motion, a and v are not parallel - nor are they in projectile motion, where the acceleration a = g is always downward but the velocity vector can have various directions.
Circular motion is often described in terms of the frequency f as so many revolutions per second. The period T of an object revolving in a circle is the time required for one complete revolution. Period and frequency are related as follows:
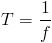
For example, if an object revolves at a frequency of 3 rev/s, then each revolution takes 1/3 s. For an object revolving in a circle at a constant speed v, we can write
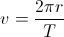
since in one revolution the object travels one circumference (= 2πr).
A 150 g ball at the end of a string is revolving uniformly in a horizontal circle of radius 0.600 m. The ball makes 2.00 revolutions in a second. What is the centripetal acceleration?
SOLUTION The centripetal acceleration is aR = v2 / r. First we need to determine the speed of the vall v. The ball makes two complete revolutions per second, so its period is T = 0.500 s. In this time it travels one circumference of the circle, 2πr, so the ball has speed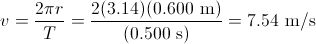
The centripetal acceleration is
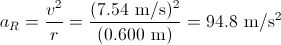
The Moon's nearly circular orbit about the Earth has a radius of about 384,000 km and a period T of 27.3 days. Determine the acceleration of the Moon toward the Earth.
SOLUTION In orbit around the Earth, the Moon travels a distance 2πr, wherer = 3.84 X 108 m is the radius of its circular path. The speed of the Moon in its orbit about the Earth is v = 2πr / T. The period T in seconds is T = (27.3 d)(24.0 h/d)(3600 s/h) = 2.36 X 106 s. Therefore,
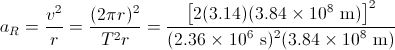
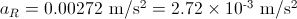
We can write this in terms of g = 9.80 m/s2 (the acceleration of gravity at the Earth's surface) as
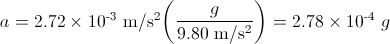
1.) An airplane is traveling 635 km/h in a direction 41.5o west of north. (a) Find the components of the velocity vector in the northerly and westerly directions. (b) How far north and how far west has the plane traveled after 3.00 h?
[Show Answer]
2.) Determine the magnitude and direction of the sum of the three vectors
V1 = 4i - 8j, V2 = i + j, and V3 = -2i + 4j.
[Show Answer]
3.) A diver running 2.1 m/s dives out horizontally from the edge of a vertical cliff and reaches the water below 3.0 s later. How high was the cliff and how far from the base did the diver hit the water?
[Show Answer]
4.) A football is kicked at ground level with a speed of 18.0 m/s at an angle of 32.0o to the horizontal. How much later does it hit the ground?
[Show Answer]
5.) A shotputter throws a shot with an initial speed of 14.0 m/s at a 40o angle to the horizontal. Calculate the horizontal distance traveled by the shot if it leaves the athlete's hand at a height of 2.2 m above the ground.
[Show Answer]
6.) The pilot of an airplane traveling 160 km/h wants to drop supplies to flood victims isolated on a patch of land 160 m below. The supplies should be dropped how many seconds before the plane is directly overhead?
[Show Answer]
7.) A projectile is fired with an initial speed of 51.2 m/s at an angle of 44.5o above the horizontal on a long flat firing range. Determine (a) the maximum height reached by the projectile, (b) the total time in the air, (c) the total horizontal distance covered (that is, the range) and (d) the velocity of the projectile 1.50 s after firing.
[Show Answer]
8.) A high diver leaves the end of a 50.0 m high diving board and strikes the water 1.3 s later, 3.0 m beyond the end of the board. Considering the diver as a particle, determine (a) her initial velocity, (b) the maximum height reached, and (c) the velocity with which she enters the water.
[Show Answer]
9.) The cliff divers of Acapulco push off horizontally from rock platforms about 35 m above the water, but they must clear rocky outcrops at water level that extend out into the water 5.0 m from the base of the cliff directly under their lauch point. What minimum push off speed is necessary to do this? How long are they in the air?
[Show Answer]
10.) A ball is thrown horizontally from the top of a cliff with initial speed v0
(at t = 0). At any moment, its direction of motion makes an angle θ to the horizontal. Derive a formula for θ as a function of time, t, as the ball follows a projectile's path.
[Show Answer]
11.) A jet plane traveling 1800 km/h (500 m/s) pulls out of a dive by moving in an arc of radius 3.50 km. What is the plane's acceleration in "g's"?
[Show Answer]
12.) What is the centripetal acceleration of a child 3.6 m from the center of a merry-go-round if the child's speed is 0.85 m/s?
[Show Answer]
13.) Calculate the centripetal acceleration of the Earth in its orbit around the Sun. Assume the Earth's orbit is a circle of radius 1.5 X 1011 m.
[Show Answer]
14.) What si the magnitude of the acceleration of a speck of clay on the edge of a potter's wheel turning at 45 rpm (revolutions per minute) if its diameter is 30 cm?
[Show Answer]
15.) Suppose the space shuttle is in orbit 400 km from the Earth's surface, and circles the Earth about once every 90 minutes. Find the centripetal acceleration of the space shuttle in its orbit. Express your answer in terms of g, the gravitational acceleration at the Earth's surface.
[Show Answer]







