We begin our little journey through the realm of physics with one dimensional kinematics. Kinematics is the study of the motion of objects. This subset of Mechanics has been contributed to greatly by physicists such as Galileo Galilei (1564-1642) and Isaac Newton (1642-1727). When restricted to motion in a straight line path objects are said to be moving in one dimension. Although this seems overly simplistic for science, it actually comes in handy in many situations and especially so when the motion of an object can be broken down into components each of which involves one of the two or three dimensions being considered. We will encounter situations such as this soon enough. For now let us just be concerned with the topic at hand.
Measurements of position, speed, and distance are done with respect to to what is refered to as a Reference Frame. Take for example the experience of riding in a car on the highway. When you look out the window you may see cars that seem to hold the same position in relation to you, while others seem to be falling behind or racing ahead. This happens because the cars that seem to be holding position relative to you are moving at the same speed with respect to an observer not moving at all on the side of the highway. The cars falling behind or racing ahead are not. Another example I can give you is the measurement of someone running on a train by an observer on the train and one who is standing by the tracks. The observer on the train will measure the runner's speed to be one value, lets say v1, while the observer next to the tracks will measure the runner's speed to be another value, lets say v2. Now lets say the speed of the train is v. Then v2 will be v2 = v + v1. Of course, this assumes the runner is moving in the same direction as the train.
When we speak of the motion of an object we are not only concerned with the speed of the object but the direction in which it is moving. This can be specified using coordinate axes to represent the object's frame of reference. In physics we use the all too familiar cartesian coordinate axes. In three dimensions this consists of the usual x, y, and z axes. In one dimension we are only concerned with the x axis however. It is on this axis that the position of an object is given by its x coordinate at any moment.
Now we should make a distinction between the distance an object has traveled, and its displacement, which in physics is defined as the change in position of the object. For example, if a person walks in one direction 100 meters and then turns around and walks 20 meters then his/her displacement from the starting point is only 80 meters while his/her distance traveled is 120 meters. Displacement is a quantity that incorporates both magnitude and direction and we represent such quantities with vectors, which are basically arrows in diagrams. We will explore vectors more fully later. Lets move on now.
The most evident thing we tend to notice when we are studying the movement of an object is its speed. In physics we define speed as how far an object travels in a given time intervel, regardless of its direction. The average speed of an object is defined as the total distance traveled along its path divided by the time it takes to travel this distance:
We should make a distinction between the terms velocity and speed. Velocity in physics is a vector quantity, while speed is not. Also, the average velocity of an object is defined in terms of displacement, rather than total distance traveled. Average velocity is defined as the following:
More descriptively, the equation for average velocity can be written as follows:
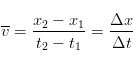
v stands for velocity and the bar above it is the standard symbol for "average." x2 is the final position of the object and x1 is the initial position. t2 is the final measured time and t1 is the starting time. The triangle you see before the x and the t is the greek letter delta which usually denotes change.
How far can a cyclist travel along a straight road if he/she is moving at an average velocity of 18 km/h for 2.5 h?
SOLUTION We want to determine the distance traveled, so we can use the above equation like so:
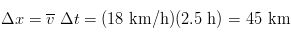
When we were discusiing the topic of average velocity it was refered to as such because over a given time intervel it may be the case that the objects velocity flucuates. That is, it may speed up and/or slow down over the given time intervel. To describe such a situation when need to introduce the concept of instantaneous velocity, which is the velocity of the object at a given instant in time. We can think of this quantity as the average velocity over an infinitesimally short time interval. Thus instantaneous velocity can be defined as such:
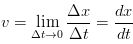
From this point forth when we refer to the velocity of a moving object it will be the object's instantaneous velocity that we are refering to. If we instead are speaking of an object's average velocity it will be made explicit that is what we are talking about. Note that instantaneous speed will always refer to the magnitude of the object's instantaneous velocity. Why, you may ask? Because at infinitesimally small values distance and displacement are the same. Now, as defined above, in order to find the instantaneous velocity of an object we need to define its position as a function of time. The following example will demonstrate how to find an object's instantaneous velocity.
A jet engine moves along an experimental track in one direction (which we will call the x-axis). Its position as a function of time is given by the equation x = At2 + B, where A = 2.10 m/s2 and B = 2.80 m. (a) Find the displacement of the engine during the time intervel from t1 = 3.00 s to t2 = 5.00 s. (b) Determine the average velocity during the given time intervel. (c) Finally, compute the magnitude of the instantaneous velocity at t = 5.00 s.
SOLUTION (a) At t1 = 3.00 s, the position of the engine is
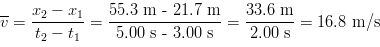
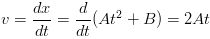
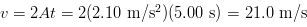
When an object that is moving changes its speed and/or direction it is undergoing an acceleration. Average Acceleration is defined as the change in velocity divided by the elapsed time in which the change in velocity took place as follows:
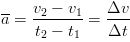
I don't know if you realized it but the term A in the position function of the jet engine indicated its velocity was changing over time. This is evidenced by the units m/s2, which denotes meters per second per second. This means that the velocity was changing by the amount A every second.
Like with velocity, acceleration can be nonconstant. This means the acceleration can be changing over time and thus the acceleration at a given moment is its instantaneous acceleration, which is defined as follows:
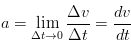
From now on when we refer to "acceleration" it will be instantaneous acceleration we're speaking of. If we instead are talking about average acceleration it will be made explicit. Now lets move on.
There are many situations where there is constant acceleration or assuming constant acceleration will produce accurate enough results. One such example is the acceleration of a falling object near the surface of the earth. If the motion of an object is in a straight line and its acceleration is constant there are four equations that are very useful when studying the motion of the object. We will now derive and list those equations. Of course, if the acceleration is constant the average acceleration and instantaneous acceleration are the same. We will set the initial time t1 to 0 and initial values of x and v wil be noted with a subscript of 0 which in spoken word is pronounced "EX NOT" and "VEE NOT" and final values will have no subscript.
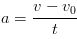
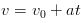
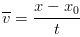
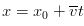
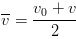
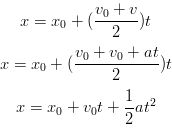
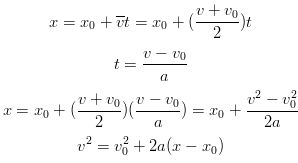
So, without further ado, the four equations we derived that will prove to be very useful in kinematics and upcoming topics are listed below.
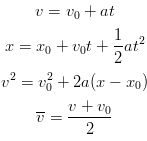
Please remember that the above equations are only useful when the acceleration of the object being considered is constant. So, tuck these gems of kinematics away because we will be using them quite a bit.
Imagine that you are designing a runway for an airport that will be used by small planes. One kind of small aircraft that will be using this airport must reach a speed of 27.8 m/s to take off and is capable of accelerating at a rate of 2.00 m/s2. (a) If the runway is 150 m long, can this airplane reach the needed speed to takeof? (b) If not, what minimum length must the runway have?
SOLUTION (a) We know the airplane's acceleration and the travel distance available for takeoff. What we need to know is if the plane can reach its minimum takeoff speed given ths information. We can determine this from the additional knowledge that the aircraft's initial speed and position is 0 as follows:
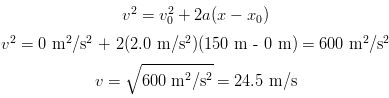
Obviously, 24.5 m/s is less than 27.8 m/s. So, the runway is not long enough.
(b) Now we must figure out the minimum length the runway must be to reach
27.8 m/s. This can be done as follows:
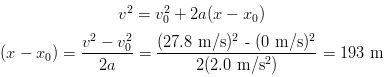
A motorcyclist starts from rest on a road and accelerates at a rate of 0.5 m/s2 for a distance of 120 m in a 15 m/s zone. Does the cyclist end up breaking the speed limit by the time he reaches the 120 m point?
SOLUTION The answer is quite easily computed as follows:
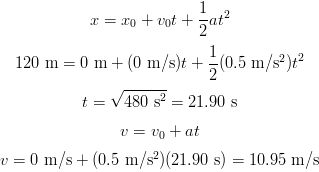
The answer is no. The motorcyclist is not speeding by the time he reaches 120 m. But he will if he continues accelerating at that rate.
Estimate the minimum stopping distance of a car given the reaction time of the driver is 0.50 s, the acceleration of the car once the brakes are applied is -6.0 m/s2, and the initial velocity of the car is 14 m/s.
SOLUTION First we calculate the distance traveled by the car during the reaction time, and then use that as x0 in the next equation we make use of.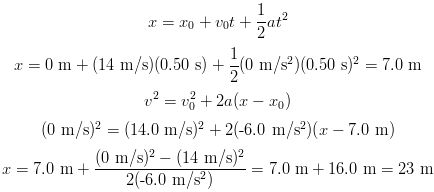
As mentioned earlier objects falling near the surface of the earth can be considered to be experiencing uniformly accelerated motion. This means the equations we derived in the last section can prove to be useful in situations involving objects falling due to gravity. The magnitude of the acceleration of a falling object due to gravity near the surface of the earth is approximately as follows:
To be more accurate, the acceleration due to gravity does vary slightly according to latitude and elevation, but these variations are so small they can be ignored during calculations with an extremely minimal amount of error. Well, lets now see some example problems involving falling objects.
Suppose a person is atop a tower that is 70.0 m high and throws a ball vertically downward at an initial velocity of 3.00 m/s. Take downward to be motion in the positive direction and along the y axis. (a) What would be its position after 2.00 s? (b) What is its velocity after 2.00 s?
SOLUTION (a) The answer can be easily calculated knowing the acceleration of gravity as follows:
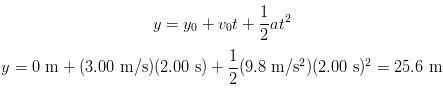
(b) And this part of the answer is easily computed as well.
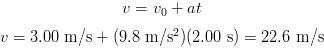
A person throws a ball upward into the air with an initial velocity of 15.0 m/s. Calculate (a) how high the ball goes, and (b) how long the ball is in the air until it comes back to the thrower's hand.
SOLUTION Lets choose y to be positive in the up direction. The key to solving this problem is realizing that the ball's velocity is zero when it reaches its highest point and that the accleration of the ball is due to gravity which is in the opposite direction of the ball's motion until it reaches its apex. So, lets take the initial y position to be zero. (a) The highest point can be calculated as follows:
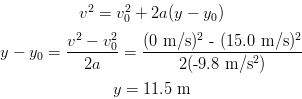
(b) Now we need to determine how long the ball is in the air before it returns to the person's hand. We could do this by breaking the problem into two parts in which we calculate the time it takes the ball to reach it highest point and then calculate how long it takes the ball to fall back to the thrower's hand. We would then add the two time intervels together to get the answer. Another approach is to just consider the overall motion from the beginning point at which y is at 0 m to the ending point at which y is again at 0 m. The calculation would be as follows:
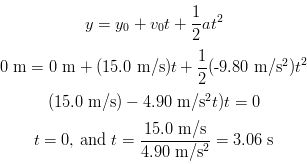
t = 0 s corresponds to the moment at which the ball is first thrown upward and t = 3.06 s corresponds to the time at which it returns to the thrower's hand. So, the answer is t = 3.06 s.
Let's consider once again a ball thrown upward under the exact same conditions as in the last example, and let us make three more calculations. (a) Calculate how much time it takes for the ball to reach its highest point, (b) the velocity of the ball when it returns to the thrower's hand, and (c) at what time t the ball passes a point 8.00 m above the person's hand.
SOLUTION (a) Again, take y as positive upward. The answer can be calculated as follows:
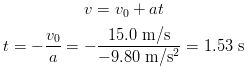
(b) We can use the same equation to obtain this answer if we remember the time that elapses before the ball returns to the thrower's hand. Bear in mind what positive and negative quantities mean.
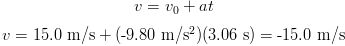
(c) What we want here is t given y = 8.00 m, y0 = 0 m, v0 = 15.0 m/s, and
a = -9.80 m/s2.
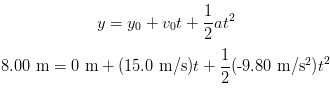
This is a quadratic equation. To solve any quadratic equation of the form
at2 + bt + c = 0, where a, b, and c are constants, the quadratic formula gives the solutions
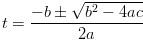
So, when we rewrite the expression in the standard form the computation is as follows:
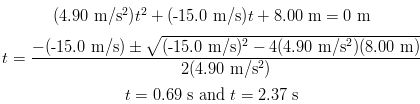
The two answers to this part of the problem are valid because the ball passes the 8.00 m point twice. Once on the way up and again on the way down.
Now, in the next example we're going to see how to go about dealing with changing acceleration. This involves returning to the basic definition of acceleration and using a little integral calculus. This material will not show up in the prolem set for one dimensional kinematics and is purely for the reader's benefit.
An experimental vehicle starts from rest and accelerates at a rate given by a = (7.00 m/s3)t. What is (a) its velocity and (b) its displacement 2.00 s later?
SOLUTION (a) None of the equations we derived earlier are applicable because they are only valid in situations where acceleration is constant. If you recall the definition of acceleration is
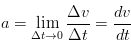
This equation can be algebraically manipulated so dv = a dt. If we then take the definite integral of both sides where the left side integral is taken from v = 0 to the final velocity v. The right side integral would then correspondingly be taken from t = 0 to an arbitrary time t. Remember what the equation for acceleration is in this problem. The calculation would then be as follows:
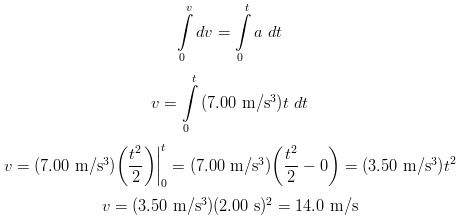
(b) To obtain the displacement we remember the definition of velocity which is
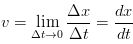
Now, to get the answer we rearrange the equation to dx = v dt and integrate using the equation for the vehicle's velocity we found in the first part to this problem. The calculation for the displacement of the vehicle after 2.00 s is as follows:
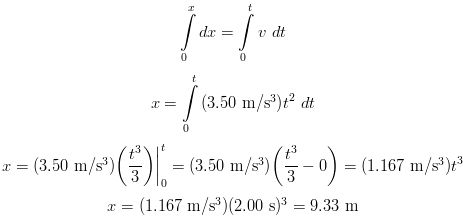
1.) A bird can fly 15 km/h. How long does it take to fly 75 km?
[Show Answer]
2.) A horse moves away from its trainer in a straight line, moving 160 m away in 17.0 s. It then returns abruptly and gallops halfway back in 6.8 s. Calculate (a) its average speed and (b) its average velocity for the entire trip, using "away from the trainer" as the positive direction.
[Show Answer]
3.) A car traveling 90 km/h is 100 m behind a truck traveling 75 km/h. How long will it take the car to reach the truck?
[Show Answer]
4.) A bowling ball moving with constant speed hits the pins at the end of a bowling lane 16.5 m long. The bowler hears the sound of the ball hitting the pins 2.50 s after the ball is released from his hands. What is the speed of the ball? The speed of sound is 340 m/s.
[Show Answer]
5.) A sports car is advertised to be able to stop in a distance of 55 m from a speed of 100 km/h. What is its acceleration? How many g's is this
(g = 9.8 m/s2)?
[Show Answer]
6.) A light airplane must reach a speed of 32 m/s for takeoff. How long of a runway is needed if the acceleration of the airplane is 3.0 m/s2?
[Show Answer]
7.) Determine the stopping distances for an automobile with an initial speed of 90 km/h and a human reaction time of 1.0 s: (a) for an acceleration a = -4.0 m/s2; (b) for a = -8.0 m/s2.
[Show Answer]
8.) A 75 m long train accelerates uniformly from rest. If the front of the train passes a railway worker 140 m down the track at a speed of 25 m/s, what will be the speed of the last car as it passes the worker?
[Show Answer]
9.) If a car rolls from rest off a vertical cliff, how long does it take to reach 100 km/h? Neglect air resistance and remember the acceleration of gravity is g = 9.80 m/s2.
[Show Answer]
10.) A kangaroo jumps to a vertical height of 2.55 m. How long was it in the air before returning to Earth?
[Show Answer]
11.) A helicopter is ascending vertically with a speed of 5.60 m/s. At a height of 115 m above the Earth, a package is dropped from a window. How much time does it take for the package to reach the ground?
[Show Answer]
12.) A falling stone takes 0.30 s to travel past a window 2.2 m tall. From what height above the top of the window did the stone fall?
[Show Answer]
13.) The acceleration due to gravity on the Moon is about one sixth what it is on Earth. If an object is thrown vertically upward on the Moon, how many times higher will it go than it would on Earth, assuming the same initial velocity?
[Show Answer]
14.) A person who is properly constrained by an over-the-shoulder seat belt has a good chance of surviving a car collision if the deceleration does not exceed 30 "g's" (1.00 g = 9.80 m/s2). Assuming uniform deceleration of this value, calculate the distance over which the front end of the car must be designed to collapse if a crash brings the car to rest from 100 km/h.
[Show Answer]
15.) Two children are playing on two trampolines. The first child can bounce up to one-and-a-half times higher than the second child. The initial speed upward of the second child is 5.0 m/s. (a) Find the maximum height the second child reaches. (b) What is the initial speed of the first child? (c) How long was the first child in the air?
[Show Answer]







